Repeat Problem 9.10 with each of the following forcing functions, and a damping ratio of zero:

a. F = 10 sin(5t)

b. F = 10 sin(10t)

c. F = 10 sin(15t)

What do you notice about part b, in which the forcing frequency is equal to the natural frequency of the system? (If you have ever driven a car with a wheel badly out of balance, you might have noticed this condition of resonance. At a certain speed, the vibrations will be much more noticeable than at lesser or greater speeds. At this speed, the frequency of the rotating tire is nearly equal to the natural frequency of the car.)

Problem 9.10

Write a MATLAB file which utilizes the function written in Problem 9.9 to calculate and plot the displacement for values of time from 0 to 5 seconds. Use 1,000 intervals of time. Comment on the shape of the curve. Repeat for values of the damping ratio of 0 (undamped) and 0.5.

Problem 9.9

In Chapter 5, we plotted the free vibration of a spring-mass-damper system. Often, we want to analyse the response of the system to forced vibrations. This system is illustrated in Figure P9.9.

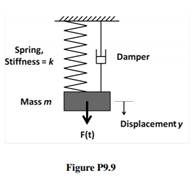
The forcing function here is simply the weight of the mass. The physical interpretation of the problem is that initially, the mass is being held at rest, at the position where the spring is at its free length. At time t = 0, the mass is dropped, hence the force of the weight is applied instantaneously.

Use 1,000 increments of time from 0 to t1. Consider writing a separate MATLAB function for the force as a function of time, so that it can be changed easily in later problems.

Check your function with these values:

Note that as time increases, the displacement approaches the equilibrium position, which is calculated as the weight divided by the spring stiffness.