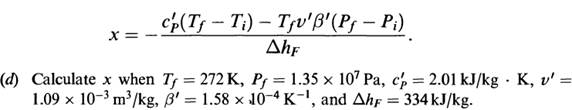on is known as regelation. Heat, therefore, is liberated above the bar, is conducted through the metal and a layer of water under the metal, and is absorbed by the ice under the layer of water. Show that the speed with which the bar sinks through the ice is
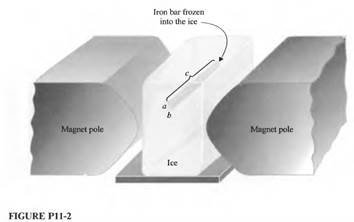
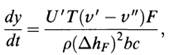
Where U’ is the overall heat-transfer coefficient of the composite heat-conducting path consisting of the metal and the water layer. U’ is given by
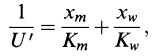
Where Xm and Xw are the thicknesses of the metal and water layer, respectively, and Km and Ki are their respective thermal conductivities.
(c) Assuming that the water layer has a thickness of about 10-5 m and a thermal conductivity of about 0.6 W/m· K, and that the bar is 0.1 m long, with a and b each equal to 10-3 m, with what speed will the bar descend when F = 102 N? (Thermal conductivity of steel is 60W/m· K.)
Problem 11.12
Figure P11-1 shows the surface for the equation of state of water as viewed from the high-temperature end. Consider Ikg of ice in the state i (Pi = 1.01 x 105 Pa, Ti = 273K).
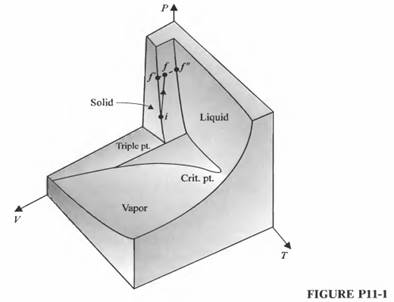
The ice experiences an isentropic compression to a state f:
(a) Why is the state f in the mixture region? In other words, why does some of the ice melt?
(b) Show that the fraction x of ice that is melted is given by
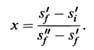
(c) State explicitly the simplifying assumptions that must be made in order that x may be written