The standard parabolic wave equation can be derived by introducing a narrowangle approximation to a modal representation of the field in a waveguide. Let the modal solution be given by
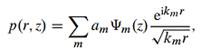
where the eigenfunctions 
satisfy the depth-separated wave equation
Here, k0 is the reference wavenumber and 
the index of refraction. By assuming the modal eigenvalues to cluster around k0 (a narrow-angle approximation) and to be given in the form 
where 
is small compared to unity, show that to leading order in 
the field solution can be written in the for
where the envelope function 
satisfies the standard parabolic equation (6.9).
