The data in the following  come from an experiment to study the effects of temperature (factor A), processing time (factor B), and the rate of temperature rise (factor C) on the amount dye (the response variable) left in the residue bath of a dyeing process. The experiment was run at two levels for each factor, with two replicates at each factor-level combination.

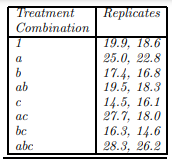
(Source: Milton and Arnold (1990), Introduction to Probability and Statistics, 2nd. ed., McGraw-Hill, New York. Used with permission.) (a) Prepare a  similar in format listing all the contrasts and estimates of the main effects and interactions. (b) Using the results obtained in part (a) compute the sums of squares for each main and interaction effect. (c) Given the information that SST = 313.88 and SSE = 56.14 compute the proportion of the total variability explained by each main effect and interaction. Rank the effects in decreasing order of importance as measured by SS(effect)/SST. (d) Using the information obtained in parts (b) and (c) compute the ANOVA  in a format similar. Are your final results consistent with the preliminary conclusions you obtained in part (c)? Comment.