An infinite elastic plate of thickness 2h is made of an elastic material with wave speeds cp and cs for compressional and shear waves, respectively, and density _s. The plate is assumed to have free surfaces.

a. Show that the characteristic equation for the modes in the plate has the form

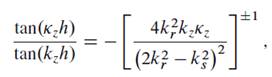
where the “C” corresponds to symmetric modes and the “_” corresponds to antisymmetric modes. ks is the shear wavenumber, and kz and z are the vertical wavenumbers for compression and shear, respectively. kr is the horizontal wavenumber.

b. Show that in the low-frequency limit,

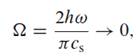
the characteristic equations reduce to,

where _ is a dimensionless horizontal wavenumber,

c. Solve the frequency equation numerically and graphically represent the ! _ kr relations for the first (fundamental) symmetric and antisymmetric modes for the elastic plate.

d. Discuss the cutoff properties and the static limits of the phase and group velocities for the two fundamental modes.