In his paper “Do Dogs Know Calculus?”,1 mathematics professor Timothy Pennings made an interesting observation while playing catch with his Welsh Corgi, Elvis. Standing on the shore of Lake Michigan (point A in Figure P10.14), Pennings threw a tennis ball into the lake (point B). Rather than swimming directly toward the ball (Path a) or running along the beach and swimming the shortest distance to the ball (Path b), Elvis seemed to be optimizing his path (Path c) so that he minimized the time required to get to the ball, taking into account that he could run faster than he could swim.

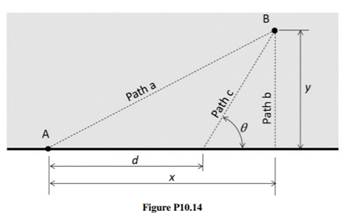
a. Use Excel Solver to determine how far Elvis should run down the beach (distance d) in order to minimize the time required to get to the ball if:

■ Elvis can run at 6.40 m/s,

■ Elvis can swim at 0.91 m/s,

■ x = 30 m, and

■ y = 10 m.

Also determine the angle θ that the path makes relative to the shoreline.

b. Repeat the problem for x = 20 m and y = 15 m.

Notes: In Penning’s analytical solution, he noted that the angle θ is dependent on the relative speeds only, and is therefore independent of x and y. He also found that Elvis’s paths did indeed match the optimal paths quite well.