Consider the problem of a water halfspace with sound speed c1 and density _1 overlying an elastic halfspace with compressional speed cp, shear speed cs, and

density _2.

a. Show that the depth-dependent Green’s function for a point source in the water,

at height H above the interface, has a denominator of the form,

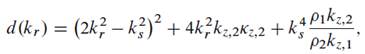
where ks is the shear wavenumber in the solid half space, kr is the horizontal wavenumber and kz;1 and kz;2 are the vertical wavenumbers for compressional waves in the two media, and z;2 is the vertical wavenumber for shear waves.

b. Show that d.k/ always has a real root kSCH,

where k1 is the wavenumber for acoustic waves in the water. The wave associated with this pole is called the Scholte wave.

c. Describe the frequency dispersion characteristics of the Scholte wave.

d. Make a sketch of the particle displacement associated with the Scholte wave on

the surface of the elastic medium.

e. Assume the source is placed just above the bottom  and emits a broadband signal. The field is measured by means of a bottom mounted vertical array far away from the source, where the field is dominated by the Scholte wave. If the frequency spectrum measured at the receiver on the interface is F.!/, what is the frequency spectrum at height h above the interface?