On a small island there are supermarkets A, L, S and W. In the current year, 30% of customers buy groceries from A, 20% from L, 40% from S and 10% from W. However, each year,

A retains 80% of its customers but loses 10% to L, 5% to S and 5% to W.

L retains 90% of its customers but loses 5% to A and 5% to S.

S retains 75% of its customers but loses 10% to A, 10% to L and 5% to W.

W retains 85% of its customers losing 5% to A, 5% to L and 5% to S.

(a) If the original market share is represented by the column vector

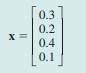
and the matrix representing the transition in supermarket loyalty is

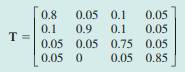
work out the matrix product, Tx, and give an interpretation of the elements of the resulting vector.

(b) Assuming that the same transition matrix applies in subsequent years, work out the percentage of customers who buy groceries in supermarket L after

(i) two years (ii) three years