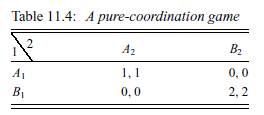
There are two individuals playing repeatedly the game whose payoffs are as specified in Table 11.3. Player i ’s admissible strategies _i consist of the countable set {γi1, γi2, γi3, . . .} ∪ {γi∞} where each γik (k ∈ N) is interpreted as follows:
“Switch irreversibly to Bi at k, provided the opponent has not switched to Bj before; in the latter case, remain playing Ai for ever.” and γi∞ is interpreted as
“Never choose Bi .” Let βo i stand for the initial beliefs of player i over j ’s strategy, with βo
Iq (q = 1, 2, . . . . ,∞) indicating the subjective probability associated with each γjq . Further assume that βo iq > 0 for each i and every q = 2, 3, . . . ,∞.Within the theoretical framework proposed in Subsection 11.4.3, answer the following questions.
(a) Does the setup described satisfy (GT)?
(b) Argue that, if (EPM) holds, some player switches to Bi at some t.
(c) Specify conditions on βo i guaranteeing that both players switch to Bi at
t = 1.
(d) Assume that (EPM) holds. Does the process converge to Nash play for the repeated game? and for the stage game? Relate your answer to (a) and Theorem 11.8.

