Consider the following mean-square differential equation,
driven by a WSS random process 
with psd
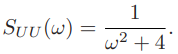
The differential equation is subject to the initial condition 
, where the random variable 
has zero-mean, variance 5, and is orthogonal to the input random process .
(a) As a preliminary step, express the deterministic solution to the above differential equation, now regarded as an ordinary differential equation with deterministic input 
and initial condition 
, not a random variable. Write your solution as the sum of a zero-input part and a zero-state part.
(b) Now returning to the m.s. differential equation, write the solution random process 
as a mean-square convolution integral of the input process over the time interval 
plus a zero-input term due to the random initial condition . Justify the mean-square existence of the terms in your solution.
(c) Write the integral expression for the two-parameter output correlation function 
over the time intervals 
. You do not have to evaluate the integral.
