A 1 cm × 1 cm square ultrasound transducer, submerged in oil, is centered at the origin and pointed down the +z-axis, as shown in Figure P11.5. A large layer of fat begins at z0 = 20 cm, and extends to infinity, so that the only possible echoes are those from the interface between oil and fat. Suppose the transducer operates at 1 MHz and the density, speed of sound, and absorption coefficient of oil and fat are:
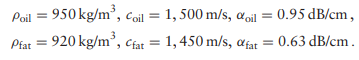
Figure P11.5 See Problem 11.13.
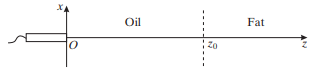
Assume that the transducer is sensitive to at most L = 65 dB pressure amplitude loss.
(a) What is the depth of penetration inside the oil?
(b) What is the approximate beamwidth at the given oil/fat interface?
(c) Suppose the peak acoustic pressure of the generated pulse is 20 N/cm2. Compute the peak pressure of the returning pulse. Is it detectable by the transducer system? Does this result conflict with the answer in part (a)? Explain why or why not
Now, assume that the interface is not fixed; instead, it is given by z0(t) = 20 − 5 cos(2πf0t) cm, where f0 = 100 Hz.
(d) Assume that the transducer fires a pulse at t = 0. Sketch the A-mode signal. Label the axes carefully, and identify the time-of-return of the returning pulse.
(e) Assume that the transducer fires every 10 ms starting from t = 0. Sketch the M-mode image that would be generated. Label the axes carefully

