(i) In a spirit similar to that of Exercise 12.9, now assume that the mutation

probabilities may depend on the prevailing state so that there is some

smooth function φ : [0, 1) × _ → [0, 1), where εω = φ(ε, ω) is the mutation

probability at state ω when the base parameter reflecting the overall

noise of the system is ε. (For simplicity, assume all players mutate with the

same probability.) Further suppose that φ(0, ·) = 0 and, as the counterpart

of (12.62), we have that

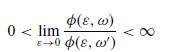
for each ω,ω

_ *_. Focus on the context in which the population plays

a bilateral coordination game under global interaction and show that the

results established in the text are not affected by the proposed variation.

(ii) Now consider a situation such as the one described in (i) above but, instead

of (12.63), suppose φ(ε, ω) = ε for all ω _= ωα but

for some r * N. Given n (the population size), characterize the values of

r that lead to the same selection result (i.e., the same stochastically stable

state) as in the text. What happens for other values of r?