Consider the imaging problem in Problem 13.3. Assume the effective spin density within the cube is constant and equal to 1.

(a) Refer to Figure P13.1 and sketch the 2-D function f(x, y) that you will image. Also sketch |F(u, 0)|.

You use the gradient echo pulse sequence shown in Figure P13.9 to image the slice with gradient G_x = 0.5 G/mm and Gy = 0.

(b) Find the duration (in seconds) of the x-gradient preceding the readout gradient in order to collect data in the range −0.4 cm⁻¹ ≤ u ≤ 0.4 cm⁻¹.

(c) How long (in seconds) after the gradient G_x changes sign will the gradient echo occur and why?

(d) After reconstructing the data collected during the acquisition, will we able to get a perfect reconstruction of g(, 0◦), where g(, θ) is the Radon transform of f(x, y)? Explain

Figure P13.9

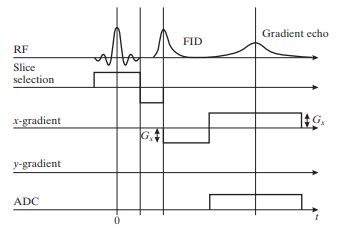
Figure P13.9 Pulse sequence for Problem 13.27.

Problem 13.3

You intend to image one slice (z = 5 cm,  z = 1 cm) of an off-centered cube having width 10 cm as shown in Figure P13.1. You are given G_z = 1 G/mm and − = γ 4.258 kHz/G.

Figure P13.1 See Problem 13.3.

(a) Find the bandwidth (in Hz) of the RF waveform needed to perform the slice selection.

(b) Give a mathematical expression for the RF waveform B₁(t) (in the rotating frame) that is needed to perform the slice selection.