A portion of a linear array is shown in Figure P10.2. Note that h > w. The array is composed of five transducers (called elements), whose faces are contained in the x-y plane and vibrate in the z direction. Assume the far-field (Fraunhofer) approximation in all of the parts below.
(a) What is the far-field pattern q0 (x, y, z) of the central element taken by itself?
(b) Find the range z0 at which the first zeros of this pattern (in the x direction) coincide with x = −s and x = +s?
(c) What condition must the separation s satisfy in order that z0 is in the far-field of the central element? (d) Find the far-field pattern q(x, y, z) of the five elements operating in unison.
(e) What is the beamwidth (out to the first zeros) of this pattern at range z0 in both the x and y directions. (Think carefully about this one before you proceed blindly ahead; it is easier than it appears at first glance.)
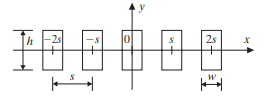
Figure P10.2 A portion of a linear array for Problem 10.17.

