Suppose a PET detector comprises four square PMTs (arranged as a 2 by 2 matrix) and a single BGO crystal with slits made in such a way that it is divided into an 8 by 8 matrix of individual detectors. Assume that the PMTs and the detectors cover the exact same square area and that each PMT is 2 in by 2 in in size. This geometry is shown in Figure P9.5. The response of a PMT to an event occurring in a particular subcrystal depends on the distance from the center of the PMT to the center of the subcrystal, r, as follows
![]()
where τ = 1 inch.
(a) Find a general expression for the response in PMT(i, j) to an event in crystal C(k, l).
(b) Find the numerical responses in each to an event in crystal C(4, 6).
(c) Ignoring the possibility of noise, develop a scheme to uniquely identify the crystal in which an event occurred.
(d) Characterize a worst-case scenario in which the smallest possible additive noise in one PMT’s signal causes an error in event localization
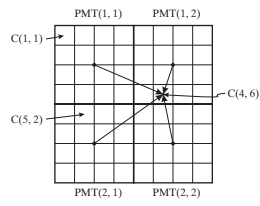
Figure P9.5 Detector geometry for Problem 9.6.

