We examine how to use nonlinearities to improve depth of penetration in ultrasound. The idea is to emit a pulse at 2.5 MHz and measure the returning echoes at the second harmonic, 5.0 MHz. Our imaging system has a dynamic range of L = 80 dB, and the tissue has an amplitude attenuation factor of μa = af dB cm⁻¹ (for  dB MHz⁻¹ cm⁻¹).

(a) Assume a tumor is located at depth d. We emit a f₀ = 2.5 MHz pulse with amplitude A₀. What is its amplitude A₁ at depth d? Answer in terms of A₀ and d.

(b) Through nonlinear interactions in the tumor, the scattered waveform is transformed into a sawtooth wave with the same amplitude A₁. It can be expressed as

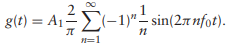
What is the Fourier transform of this waveform? Your answer will involve an infinite sum.

(c) What is the amplitude A A₂ of the sinusoidal component at f A₁ = 5 MHz at the site of the tumor? What is its amplitude A A₃ once it has traveled back to the transducer (assume a plane wave)? Answer in terms of A A₀ and d.

(d) Find the maximum value of d such that the tumor could still be detected by receiving the 5-MHz signal.

(e) Consider a traditional ultrasound system operating at f A₁ = 5 MHz. Calculate its depth of penetration.

(f) Design a convolution filter, h(t), which will remove all but the 5-MHz component of the signal g(t). It should eliminate frequencies outside the range of 4–6 MHz, and have unit gain for frequencies within that interval.