Myrtle Air Express decided to offer direct service from Cleveland to Myrtle Beach. Management must decide between a full-price service using the company’s new fleet of jet aircraft and a discount service using smaller-capacity commuter planes. It is clear that the best choice depends on the market reaction to the service Myrtle Air offers. Management developed estimates of the contribution to profit for each type of service based on two possible levels of demand for service to Myrtle Beach: strong and weak. The following table shows the estimated quarterly profits (in thousands of dollars):
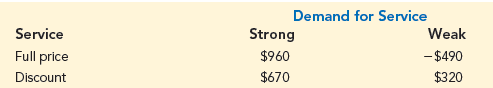
a. What is the decision to be made, what is the chance event, and what is the consequence for this problem? How many decision alternatives are there? How many outcomes are there for the chance event?
b. If nothing is known about the probabilities of the chance outcomes, what is the recommended decision using the optimistic, conservative, and mini max regret approaches?
c. Suppose that management of Myrtle Air Express believes that the probability of strong demand is 0.7 and the probability of weak demand is 0.3. Use the expected value approach to determine an optimal decision.
d. Suppose that the probability of strong demand is 0.8 and the probability of weak demand is 0.2. What is the optimal decision using the expected value approach?
e. Use sensitivity analysis to determine the range of demand probabilities for which each of the decision alternatives has the largest expected value.

