(a) Consider the linear programming problem
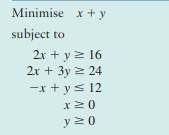
(i) Sketch the feasible region and find the exact coordinates of the corners.
(ii) Tabulate the values of the objective function at each of the corners and hence state the coordinates of the optimal point.
(iii) One of the five constraints is not needed for drawing the feasible region. State the redundant constraint.
(b) What can you say about the solution if the problem is changed to one of
(i) maximising x + y
(ii) minimising 2x + y and is subject to the same constraints as part (a)? Give reasons for your answers.
(c) The objective function in part (a) is changed to
ax + 2y
where a is a positive constant. The problem remains one of minimisation subject to the same constraints as before. Find the largest value of a for which the linear programming problem has solution x = 12, y = 0. Explain your reasoning carefully

