A radioactive pellet containing a 140 keV gamma ray emitting substance with activity A mCi is placed 1 m away from an Anger camera such that one-fourth of its total disintegrations hit the detector. Assume t1/2 = 6 hours. Assume that the Z-pulse height— that is, the photopeak— is equal to the energy of the incident photon
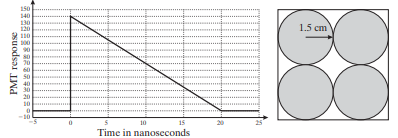
Figure P8.1 (a) (b) See Problem 8.6.
(a) What should be the acceptance window (in percentage) around the photopeak so that photons that are Compton-scattered more than 30◦ are rejected.
For the remainder of this problem, consider only non-Compton-scattered photons. Assume that the time response of the camera’s Z-pulse to an absorbed photon hitting the camera at time t = 0 is given by the plot shown in Figure P8.1(a). Assume that the response of camera is additive in nature so that its net response to multiple absorbed photons at different time instants is the shifted addition of their individual responses.
(b) Plot and label the net response of camera’s Z-pulse for two photons absorbed at time t = 0 ns and t = 5 ns.
Assume that the photon detection circuit and position logic circuit is turned on when the Z-pulse exceeds 80% of the photopeak and is turned off when the response falls below 80% of that height. A photon is considered to be accepted as an event if the maximum of the Z-pulse when the detection circuit is on falls within a 20% acceptance window around the photopeak.
(c) What is the minimum time interval between two detected photons such that they are accepted as separate events.
(d) What should be the activity of the radioactive pellet so that the chances of having at least one disintegration in the time interval given in part (c) is 50%.
Consider the arrangement of PMT’s shown in Figure P8.1(b), where the origin is at the exact center of the square. Let the responses from the four PMT tubes to a detected photon be given by 80, 30, 20, and 5 (top-left, top-right, bottom-left, and bottom-right).
(e) Compute the height of the Z-pulse and the x and y location of the event.

