Price sensitivity and convexity. It is recommended to use a spreadsheet to solve this problem.
Suppose the US zero-coupon rate curve is given as:
![]()
Consider the following three bonds with face value $100:
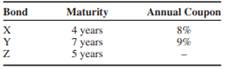
(a) Calculate the arbitrage price of each bond.
(b) The price sensitivity of a bond (also known as the ‘dollar value of one basis point’ or DV01) is defined
as the change in price when all rates go up 1 basis point (i.e. a +0.01%
parallel shift of the entire zero-coupon rate curve). Compute the price sensitivity of each bond.
(c) Calculate the price of each bond in the following scenarios:
(i) 10 basis point rate increase (+0.10%);
(ii) 1 point rate increase (+1%).
(d) Compare your respective answers to question (c) with:
(i) 10 times the price sensitivity;
(ii) 100 times the price sensitivity.
(e) Based on this comparison, do you think that price sensitivity is a good indicator of the interest rate risk which bonds are exposed to?
(f) (*) Suppose that the zero-coupon rate curve is flat at rate r. Using a second-order Taylor expansion in r, identify a secondary indicator for the interest rate risk of a bond.

