An educational researcher designs a study to evaluate the effect of providing students  with a laptop containing supplemental material to assist them in learning specified mathematical concepts. The researcher wants to also evaluate the effect of grade level of the students and their mathematical ability on the benefit of using the supplemental materials. The principals of two schools, one junior high and one high school, agree to participate in the study. Within each school, 12 classrooms are selected, with 2 classrooms randomly assigned to each of the combinations of two factors: supplemental materials (yes or no) and student math scores in the previous school years (low, medium, and high). Twenty students in each of the 24 classrooms are given a test to evaluate their mathematical proficiency both at the beginning and at the end of the semester in which the study was conducted. The difference in the two test scores will be used as the response variable to measure whether the supplemental materials provided a benefit in learning mathematical concepts. The mean responses of the students in the 24 classrooms are given in the following table.

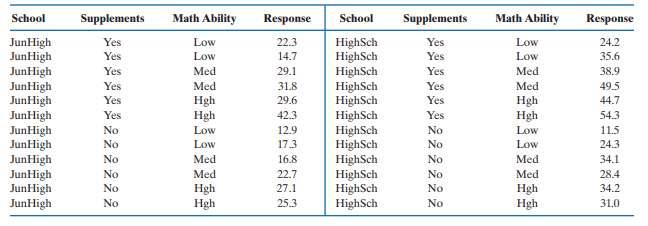
a. The researcher analyzed the data as a completely randomized experiment with two replications of the complete crossing of the three factors: type of school (junior high or high school), supplemental materials (yes or no), and math ability of the students (low, medium, or high). If possible, test for the main effects, two-way interactions, and three-way interaction of the three factors at the   .05 level.

b. If you determined that it was not possible to conduct all the tests requested in part (a), modify the analysis so that a complete analysis can be conducted on two of the three factors.