Given 
that minimize
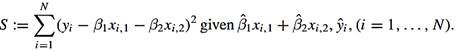
Show the following three equations.
(a)
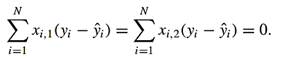
For arbitrary 
For arbitrary 
can be expressed by
(b) We consider the case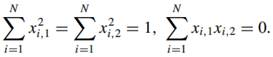 
In the standard least squares method, we choose the coefficients as 
However, under the constraint that 
is less than a constant, we choose 
at which the circle with center 
and the smallest radius comes into contact with the rhombus. Suppose that we grow the radius of the circle with center 
until it comes into contact with the rhombus that connects (1, 0), (0, 1), (−1, 0), (0, −1). Show the region of the centers such that one of coordinates 
is zero.
(c) What if the rhombus in (b) is replaced by a unit circle?
