Ignoring the inverse square law and attenuation, an approximate reconstruction for SPECT imaging is given by
![]()
where c˜(![]() ) =
) = ![]() {|
{|![]() |W(
|W(![]() )} and W(
)} and W(![]() ) is a rectangular windowing filter that cuts off at
) is a rectangular windowing filter that cuts off at![]() =
= ![]() 0. Suppose we use M projections (θ1, θ2, …, θM) uniformly spaced over the range [0, π), and N + 1 (odd) ray paths per projection. Assume the spacing between detectors is T, and gij = gθj (iT). A discrete approximation to the reconstruction of ˆ f(x, y) can be written as
0. Suppose we use M projections (θ1, θ2, …, θM) uniformly spaced over the range [0, π), and N + 1 (odd) ray paths per projection. Assume the spacing between detectors is T, and gij = gθj (iT). A discrete approximation to the reconstruction of ˆ f(x, y) can be written as
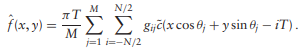
(a) The observation gij is proportional to the number of photons hitting the detector i at angle θj, Nij, that is, gij = kNij. Assume Nij is a Poisson random variable with mean Nij and is independent for different i and j. Give the mean and the variance of the reconstructed image, mean[ˆ f(x, y)] and var[ˆ f(x, y)].
(b) Show that
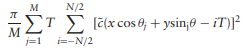
can be approximated as ![]() .
.
Now, like in CT, we assume that Nij ≈ N.
(c) Find var[ˆ f(x, y)] using the result in (b).
(d) Define SNR = ![]() . Assume that we double the photon counts, that is, N = 2N. Before doubling, the SNR is SNR1; and after doubling, the SNR is SNR2. What is the ratio
. Assume that we double the photon counts, that is, N = 2N. Before doubling, the SNR is SNR1; and after doubling, the SNR is SNR2. What is the ratio ![]() ?
?

