A planar scintigraphy calibration experiment is being performed using a uniform flood phantom. With this phantom, each pixel out of 64 × 64 pixels on an Anger camera is struck by four gamma photons per second on average.
(a) If a total count of 2,000,000 across the whole camera is considered to be a complete experiment, how long will it take (on average) to complete the calibration scan?
The burst of light from a scintillator— the Z-pulse—lasts for a brief moment every time a gamma ray hits it. Let us model this burst as a triangle with peak height A (e.g., in volts), dropping linearly to zero in 250 μs, as shown in Figure P8.8. The pulse height analyzer detects peaks and records their peak voltage. For the pulse shown in Figure P8.8, therefore, the pulse height analyzer records the value A. Assume that the response of two or more gamma rays is the sum of their Z-pulses, delayed in time according to their time-of-arrival.
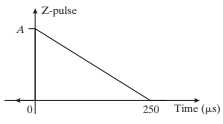
Figure P8.8 Z-pulse waveform. See Problem 8.19.
(b) Draw the combined Z-pulse arising from two photons, one striking the camera at t = 0 and the other at t = 100 μs. What will the output of the pulse height analyzer be? (It should be a sequence of heights at different times.)
Assume the photopeak is set at A and a ±20% discriminator window is used.
(c) Because of the discriminator, the second photon may not be detected if it arrives too soon after the first. Determine the time separation required in order for the second photon to be detected as a separate event.
(d) Is it theoretically possible to complete the experiment in the time you computed in part (a)? Explain.
(e) Under what condition(s) will a photon be rejected because its Z-pulse height is too small? Explain.
(f) Assume that the experiment is concluded when 2,000,000 counts are accepted no matter how long it takes. What is the intrinsic SNR in a single pixel?

