Consider the following “congestion game,” taken from Monderer
and Shapley (1996a). There are four cities located around a lake with a single road
joining them in the following clockwise order: A–B–C–D–A. There are two agents,
1 and 2, the first living in city A and the second in city B. Individual 1 wants to go
to city C, whereas individual 2 wants to reach city D. The cost of travel depends
on “congestion,” i.e., how many individuals (one or two) use the same segment of
the road joining any two adjacent cities. Costs are additive across travel segments,
with cξ (k) denoting the cost of travel segment ξ ∈ ” ≡ {AB, BC,CD, DA} when
there are k individuals using it. Model the situation as a game where each player i has two possible strategies: “travel clockwise” or “travel counterclockwise.” For any strategy profile
s = (s1, s2), define hξ (s) ∈ {0, 1, 2} as the number of individuals using segment ξ. Moreover, define the function ϒ : S → R as follows:
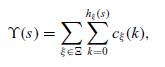
where we make cξ (0) = 0. Prove that ϒ(·) is a potential for the game described.

