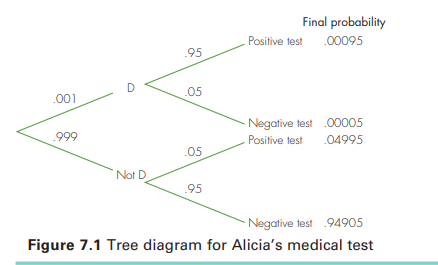
Alicia’s Possible Fates Let’s consider what could have happened with Alicia’s medical test and the probabilities associated with those options. Two random circumstances are involved. The first circumstance is whether she has the disease or not (D or not D), and the second circumstance is whether the test result is positive or negative (positive test or negative test). We have already specified the probabilities of each of the pieces, and using Rule 3a, we can find the probabilities of the various combinations, such as the probability that Alicia has the disease but the test result is negative.

Figure 7.1 illustrates these probabilities in a tree diagram. The initial set of branches shows the two possibilities and associated probabilities for her disease status. The next set of branches shows the two possibilities for the outcome of the test and associated conditional probabilities depending on whether she has the disease or not. The final probability shown for each combination of branches is found by multiplying the probabilities on the branches, applying Rule 3a. Thus, for instance, the probability that Alicia has the disease and has a positive test is .00095.

Here are the general steps for creating a tree diagram:

Step 1: Determine the first random circumstance in the sequence, and create the first set of branches to illustrate possible outcomes for it. Create one branch for each outcome, and write the associated probability on the branch. The first set of branches is the only one that contains unconditional probabilities.

Step 2: Determine the next random circumstance, and append branches for the possible outcomes to each of the branches in Step 1. Write the associated conditional probabilities on the branches, where the outcome for Step 2 is conditional on the branch taken in Step 1.

Step 3: Continue this process for as many steps (and sets of branches) as necessary.

Step 4: To determine the probability of following any particular sequence of branches, multiply the probabilities on those branches. This is an application of Rule 3a.

Step 5: To determine the probability of any collection of sequences of branches, add the individual probabilities for those sequences, as found in Step 4. This is an application of Rule 2b.